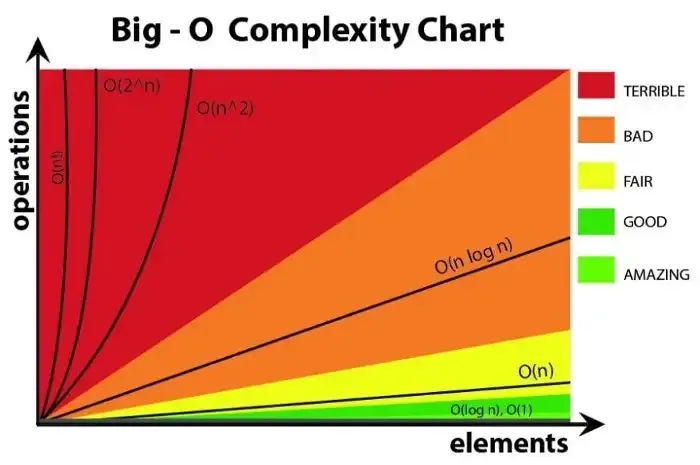
Note → Time and space complexity are high-level measures of scalability. They don’t measure the actual speed of the algorithm itself.
Time complexity in Kotlin
Time complexity is a measure of the time required to run an algorithm as the input size increases and we use Big O notation to represent it. Let’s go through the most common time complexities and learn how to identify them.
Constant Time: As input data increases, the amount of time the algorithm takes does not change.
fun checkFirst(names: List<String>) {
if (names.firstOrNull() != null) {
println(names.first())
} else {
println("no names")
}
}The size of names does not affect the running time of this function. Whether names has 10 items or 10 million items, this function only checks the first element of the list.
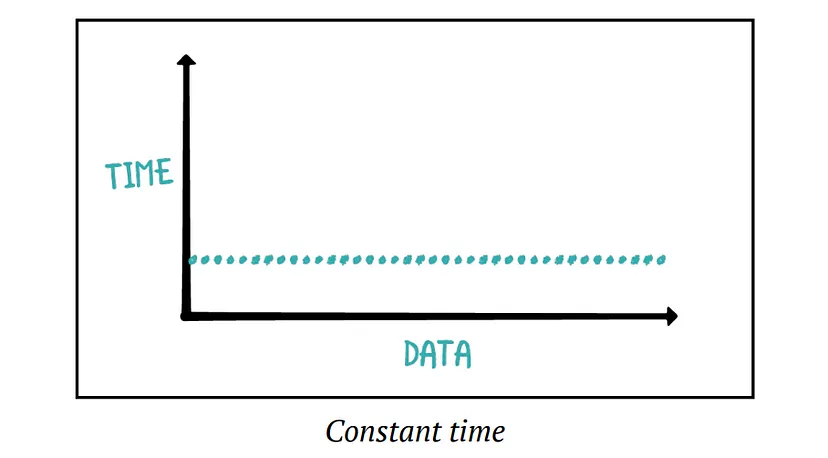
The Big O notation for constant time is O(1)
Linear Time: As the amount of data increases, the running time increases by the same amount.
fun printNames(names: List<String>) {
for (name in names) {
println(name)
}
}This function prints all the names in a String list. As the input list increases in size, the number of iterations is increased by the same amount.
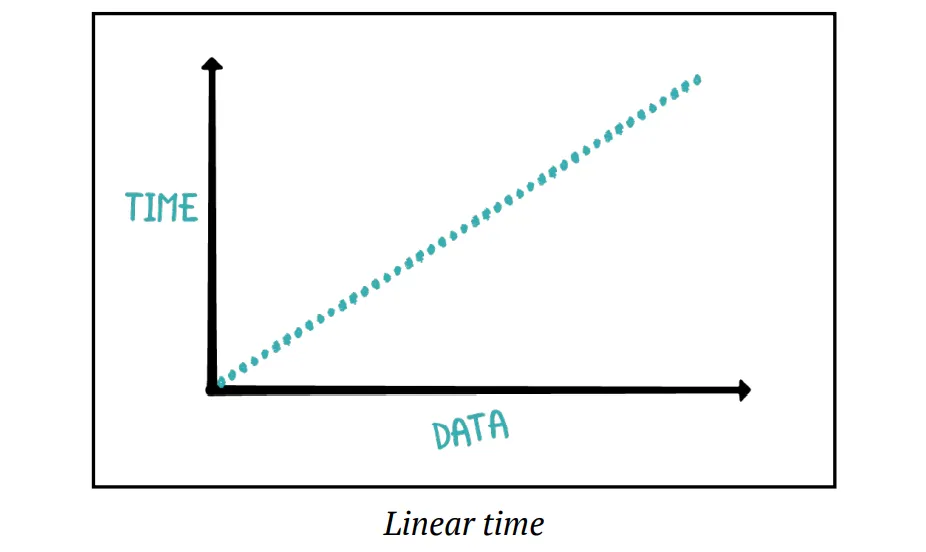
The Big O notation for linear time is O(n).
Note → All constants are dropped in the final Big O notation, In other words, O(2n + 6) is surprisingly equal to O(n).
Quadratic Time: This time complexity refers to an algorithm that takes time proportional to the square of the input size. most commonly referred to as n squared. As the size of the input data increases, the amount of time it takes for the algorithm to run increases drastically. Thus, n-squared algorithms don’t perform well at scale.
fun multiplicationBoard(size: Int) {
for (number in 1..size) {
print(" | ")
for (otherNumber in 1..size) {
print("$number x $otherNumber = ${number * otherNumber} | ")
}
println()
}
}If the input is 10, it’ll print the full multiplication board of 10 × 10. That’s 100 print statements. If you increase the input size by one, it’ll print the product of 11 numbers with 11 numbers, resulting in 121 print statements.
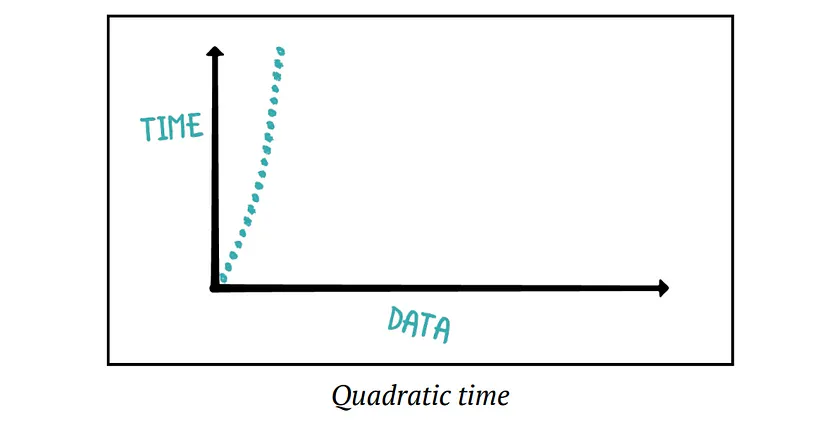
The Big O notation for quadratic time is O(n²)
Note: No matter how inefficiently a linear time O(n) algorithm is written, for a sufficiently large n, the linear time algorithm will always execute faster than a super-optimized quadratic algorithm.
Logarithmic Time: An algorithm that can repeatedly drop half of the required comparisons will have logarithmic time complexity. As input data increases, the time it takes to execute the algorithm increases at a slower rate.
fun pseudoBinaryContains(value: Int, numbers: List<Int>): Boolean {
if (numbers.isEmpty()) return false
val middleIndex = numbers.size / 2
if (value <= numbers[middleIndex]) {
for (index in 0..middleIndex) {
if (numbers[index] == value) {
return true
}
}
} else {
for (index in middleIndex until numbers.size) {
if (numbers[index] == value) {
return true
}
}
}
return false
}When you have an input size of 100, halving the comparisons means you save 50 comparisons. If the input size was 10,000, halving the comparisons means you save 5,000 comparisons.
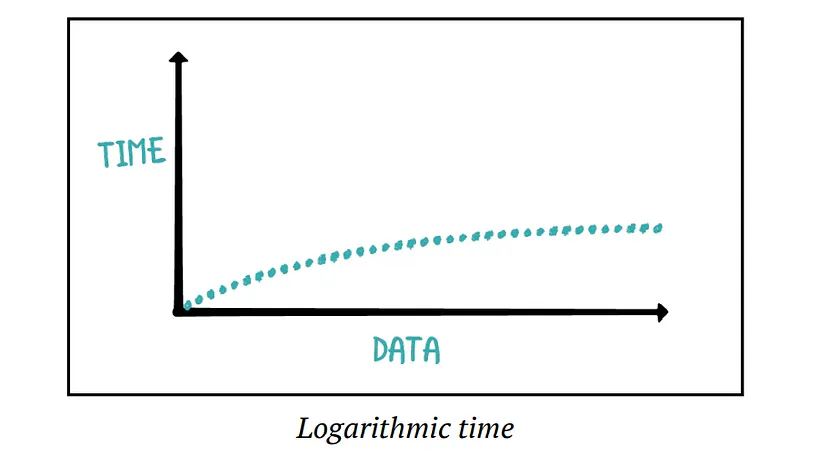
The Big O notation for logarithmic time complexity is O(log n).
Note:
Is it log base 2, log base 10, or the natural log?
In the above example, log base 2 applies. However, since Big O notation only concerns itself with the shape of the performance, the actual base doesn’t matter. The more input data you can drop after each pass, the faster the algorithm will be.
Quasilinear Time: Another common time complexity you’ll encounter is quasilinear time. Algorithms in this category perform worse than linear time but dramatically better than quadratic time. An example of a quasilinear time algorithm is Kotlin’s sort method.
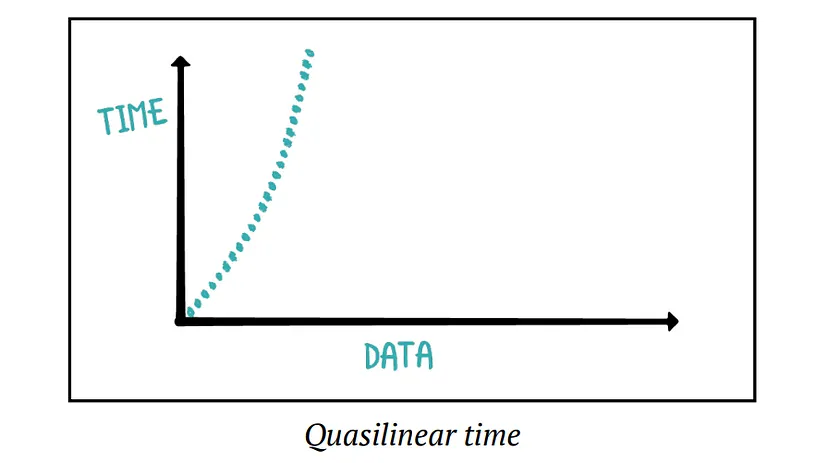
The Big-O notation for quasilinear time complexity is O(n log n) which is a multiplication of linear and logarithmic time.
Note → For small data sets, the time complexity is usually irrelevant. A quasilinear algorithm can be slower than a linear algorithm.
Other Time Complexities: Other time complexities do exist as well, these time complexities include polynomial time, exponential time, factorial time, and more.
- Polynomial — O(n²), O(n³), etc
- Exponential — O(2ⁿ)
- Factorial — O(n!)
