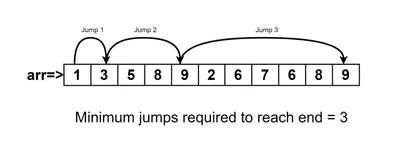
Solving problems related to array traversal and manipulation is a common task in programming interviews and competitive coding. One such interesting problem is finding the minimum number of jumps required to reach the end of an array. In this blog post, we will explore the problem, understand the underlying concepts, and implement a solution in Kotlin.

Minimum jumps Problem Statement

Problem Statement → Given an array of N integers arr[] where each element represents the max length of the jump that can be made forward from that element. Find the minimum jumps (minimum number of jumps) to reach the end of the array (starting from the first element). If an element is 0, then you can not move through that element.

Example:

Let’s consider an example to understand the problem better.

val array = intArrayOf(2, 3, 1, 1, 2, 4, 2, 0, 1, 1)

The minimum number of jumps (minimum jumps) required to reach the end of the array is 4. We can take the following jumps: 2 -> 3 -> 4 -> 1 -> 1.

Note: Return -1 if you can’t reach the end of the array.

Approach

To solve this problem, we can use a greedy approach. We start at the first element and, at each step, choose the next element that maximizes the range of reachable indices. We keep track of the current range, the next range, and the number of jumps made so far.

Solution →

1. To solve this problem we need to first break down the problem and understand it carefully.
2. Let’s assume we have a simple array → [3,4,5,2,3,1,4,2]
3. So the value at array[0] = 3, which represents the maximum or at most 3 jumps we can make towards the end of the array. that means it could be either 1 or 2 or 3. Let’s take another example array[2] = 5, here also we can jump from index 2 towards the end of the array either 1, 2, 3, 4, or 5 maximum jumps.
4. Now suppose any array element is 0 in that case, we can’t jump, so that jump path won’t be part of our optimal solution.
5. By taking care of the above two conditions, simple logic we can think that we need to iterate from the start position to till second last position in the array, why because we know from the start to the maximum position we can jump to the end of the array is second last position of the array.
6. Now the big question comes to mind how will know which jump is optimal
7. if 0 elements come somewhere in the array, will that affect our entire jump path, so to know that we will add the array index to the array element, so that, if the 0 value comes somewhere we know that our maximum jump will remain as it is, and we will skip that jump path and this is the basic logic of this problem, we need to add index and value at index in the array and then compare maximum jump reach.
8. So to solve this problem we required three variables and initially, all are zero

maxReach → it will help us to keep track of the maximum reach index we can reach from every current index in the array.

current → it will help us to keep track of the current position that we are moving ahead toward the end of the array.

jumps → it is required to find the minumum jumps( minimum number of jumps) or optimal solution to this problem.

Let’s implement this approach in Kotlin:

fun main() {
    val array = arrayOf(2, 3, 1, 1, 2, 4, 2, 0, 1, 1)

    println(findMinimumNumbersOfJumpsToEnd(array))
}

fun findMinimumNumbersOfJumpsToEnd(array: Array<Int>): Int {

    var maxReach = 0
    var current = 0
    var jumps = 0

    for (i in 0 until array.size) {   //iterate till end of array

        maxReach = Math.max(maxReach, i + array[i])  // 1

        if (current >= array.size - 1) { // 2
            break                     
        } else if (maxReach <= i) {   // 3
            return -1                 
        } else if (i == current) {    // 4
            current = maxReach
            jumps++
        }
    }

    return jumps
}

1. Here is why we add “i + array[i]”, we are adding to know that at any point our array contains any 0 value, so in such case, our maxReach will remain that particular index.
2. When our current reach to second last element of an array or beyond that, then we break the loop and return the final minimum jumps. we are handling this condition inside for loop that’s why we are not iterating for loop till the second last position in the array, otherwise, if we skip this one then, surely use array.size -1 in for loop.
3. If maxReach is i means at i index definitely 0 value presents or if below i means maxReach is behind the i, in such case, we can’t reach the end, so return -1.
4. Suppose we reached the current position (which is previously updated as maxReach) then, definitely, we found out the next maxReach index value, so now, here inside that block, we update that one, also as we are only interested in the maximum reach index among all possible jumps, that, we already found and updated in current, so we increment jumps by 1.

Conclusion

In this blog post, we explored the problem of finding the minimum jumps (minimum number of jumps) required to reach the end of an array. We implemented a solution in Kotlin using a greedy approach. This problem not only tests our algorithmic skills but also helps us understand how to efficiently traverse an array to minimize the number of steps taken.

Dry Run and Happy Coding 🙂